GRANDEZAS ESCALARES E VETORIAIS - VETORES
Existem
grandezas físicas que ficam completamente determinadas quando conhecidos os
seus valores numéricos e suas respectivas unidades de medida. Estas grandezas
são chamadas de grandezas escalares.
Ex.:
Por
outro lado, existem grandezas que , além do valor numérico e da unidade de
medida necessitam de uma direção e de um sentido para que fiquem completamente
determinadas. Estas grandezas são chamadas de grandezas vetoriais.
Ex.:
VETORES
Vetor é um ente
matemático representado por segmento de
reta orientado. O comprimento desse segmento de reta representa o valor
numérico (módulo ou intensidade do vetor); a reta suporte do segmento de reta
determina a direção do vetor; e a orientação do segmento de reta indica o sentido.
Propriedades dos vetores:
·
Um vetor pode ser deslocado no espaço, desde que
mantenha seu módulo, direção e sentido.
·
Um vetor é negativo quando o seu sentido for invertido.
OPERAÇÕES COM VETORES
1. Soma
1.1
Regra do polígono:
A regra do polígono pode
ser utilizada na adição de qualquer número de vetores. Para a sua aplicação,
devemos colocar os vetores de modo tal que: a origem do segundo vetor coincida
com a extremidade do primeiro; a origem do terceiro coincida com a extremidade
do segundo; e assim sucessivamente. O vetor resultante ou vetor soma é
determinado ligando-se a origem do primeiro à extremidade do último vetor
traçado.
1.1
Regra do paralelogramo:
A regra do paralelogramo
é aplicada somente à adição de dois vetores. Sem alterar o módulo, a direção e
o sentido de cada vetor, desenhamos os dois vetores com suas origens
coincidentes. A partir da extremidade do
vetor V1 , traçamos um segmento de reta paralelo ao vetor V2 . Em seguida, a partir da extremidade do vetor V2, traçamos um outro segmento paralelo ao vetor V1. O vetor resultante é obtido pela ligação do ponto de origem
comum dos vetores ao ponto de cruzamento dos segmentos de reta traçados.
Sendo
θ o ângulo formado entre os vetores V1 e V2, calculamos o módulo do vetor soma através da expressão:
Casos Particulares da regra do paralelogramo:
1º) Ângulo θ = 0º
Se o ângulo θ, entre o vetor V1 e o vetor V2, mede 0º, os vetores possuem mesma direção e sentido. Nesse
caso, o módulo do vetor resultante é dado pela soma dos módulos dos vetores V1 e V2.
2º) Ângulo θ = 90º
Nesse caso, o vetor V1 e o vetor V2são perpendiculares entre si. O módulo do vetor resultante é
obtido através da aplicação do teorema de Pitágoras:
3º) Ângulo θ = 180º
O vetor V1 e o vetor V2 possuem mesma direção, mas sentidos contrários. Nesse caso, o
módulo do vetor soma é dado pelo módulo da diferença entre os módulos dos
vetores V1 e V2.
2.
Subtração
Na subtração vetorial, faz-se uma soma, porém
invertendo-se um dos vetores.
Ex: V1 - V2
Conserva-se o sentido de V1 e inverte-se o sentido
de V2, somando-se os vetores logo em seguida, como na figura.
Também se
pode determinar a subtração unindo-se as origens dos vetores e traçando o vetor
diferença nas extremidades dos vetores. O vetor diferença deve apontar para o
primeiro vetor. (no exemplo o primeiro vetor seria o vetor V1)
3. Decomposição Vetorial
Um vetor pode ser escrito
como a soma de dois ou mais vetores quaisquer. Em algumas situações, podemos
decompor um vetor em suas componentes x e y, traçando retas imaginárias paralelas aos eixos que vão desde o final do vetor v até o eixo, conforme a figura abaixo.
Podemos calcular o valor de vx e vy usando trigonometria básica. Assim:
Clique aqui para baixar o texto Grandezas escalares e vetoriais
Clique aqui e acesse uma lista de exercícios de vetores com gabarito
Clique aqui e acesse uma lista de exercícios de vetores com gabarito
Clique aqui para visualizar vídeo aulas com resolução de questão sobre vetores











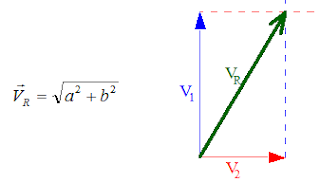








Comentários
Postar um comentário